Family to Use in Glm With Very Bimodal Data
This FAQ is an elaboration of a FAQ by Allen McDowell of StataCorp. and Nicholas J. Cox of Durham University. Please see www.stata.com/support/faqs/stat/logit.html for the original.
Proportion data has values that fall between naught and one. Naturally, it would be nice to have the predicted values also fall between aught and ane. One way to accomplish this is to use a generalized linear model (glm) with a logit link and the binomial family unit. We will include the robust option in the glm model to obtain robust standard errors which will be peculiarly useful if we have misspecified the distribution family.
We will demonstrate this using a dataset in which the dependent variable, meals, is the proportion of students receiving free or reduced priced meals at school.
use https://stats.idre.ucla.edu/stat/stata/faq/proportion, clear /* kernel density distribution of meals */ kdensity meals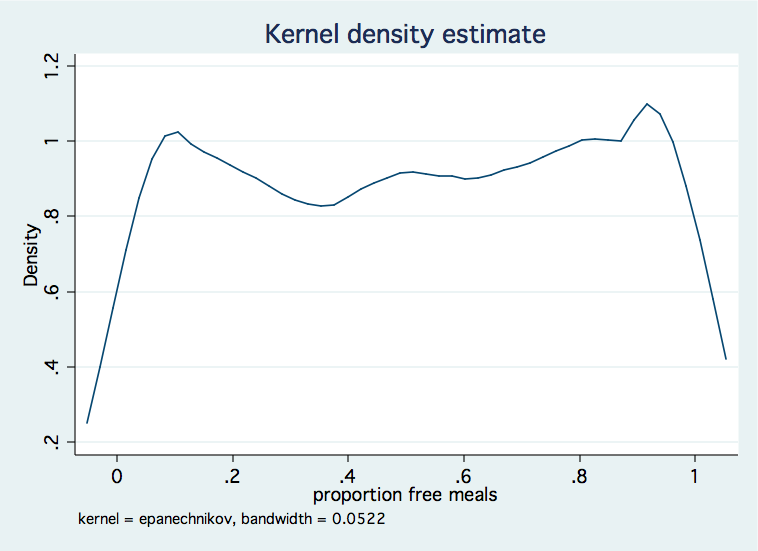
glm meals yr_rnd parented api99, link(logit) family(binomial) robust nolog note: meals has not-integer values Generalized linear models No. of obs = 4257 Optimization : ML Residual df = 4253 Scale parameter = i Deviance = 395.8141242 (1/df) Deviance = .093067 Pearson = 374.7025759 (ane/df) Pearson = .0881031 Variance function: V(u) = u*(1-u/ane) [Binomial] Link function : 1000(u) = ln(u/(1-u)) [Logit] AIC = .7220973 Log pseudolikelihood = -1532.984106 BIC = -35143.61 ------------------------------------------------------------------------------ | Robust meals | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- yr_rnd | .0482527 .0321714 i.50 0.134 -.0148021 .1113074 parented | -.7662598 .0390715 -nineteen.61 0.000 -.8428386 -.6896811 api99 | -.0073046 .0002156 -33.89 0.000 -.0077271 -.0068821 _cons | six.75343 .0896767 75.31 0.000 6.577667 vi.929193 ------------------------------------------------------------------------------
Next, we will compute predicted scores from the model and transform them back so that they are scaled the same manner every bit the original proportions.
predict premeals1 (option mu causeless; predicted hateful meals) (164 missing values generated) summarize meals premeals1 if due east(sample) Variable | Obs Mean Std. Dev. Min Max -------------+-------------------------------------------------------- meals | 4257 .5165962 .3100389 0 1 premeals1 | 4257 .5165962 .2849672 .0220988 .9770855
As a dissimilarity, let'due south run the aforementioned assay without the transformation. We volition then graph the original dependent variable and the two predicted variables against api99.
regress meals yr_rnd parented api99 Source | SS df MS Number of obs = 4257 -------------+------------------------------ F( 3, 4253) = 6752.22 Model | 338.097096 3 112.699032 Prob > F = 0.0000 Residual | seventy.985399 4253 .016690665 R-squared = 0.8265 -------------+------------------------------ Adj R-squared = 0.8264 Full | 409.082495 4256 .096119007 Root MSE = .12919 ------------------------------------------------------------------------------ meals | Coef. Std. Err. t P>|t| [95% Conf. Interval] -------------+---------------------------------------------------------------- yr_rnd | .0024454 .0054678 0.45 0.655 -.0082742 .013165 parented | -.1298907 .0048289 -26.90 0.000 -.1393579 -.1204234 api99 | -.0014118 .0000269 -52.40 0.000 -.0014646 -.0013589 _cons | 1.766162 .0134423 131.39 0.000 ane.739808 1.792516 ------------------------------------------------------------------------------ predict preols /* figure 1: proportion dependent variable */ graph twoway besprinkle meals api99, yline(0 1) msym(oh)/* figure two: predicted values from model with logit transformation */ graph twoway scatter premeals1 api99, yline(0 i) msym(oh)
/* figure iii: predicted values from model without transformation */ graph twoway scatter preols api99, yline(0 ane) msym(oh)
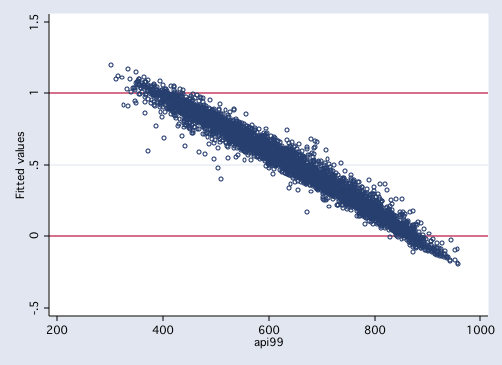
Note that the values from figures one and ii fall inside the range of zero to i while those in figure 3 the values go beyond those premises. Allow's terminate past looking a the correlations of the predicted values with the dependent variable, meals.
corr meals premeals1 preols (obs=4257) | meals premea~1 preols -------------+--------------------------- meals | 1.0000 premeals1 | 0.9152 1.0000 preols | 0.9091 0.9891 1.0000
Notation that the correlation betwixt meals and premeals1 is slightly higher than for meals and preols.
Predicting specific values
Now, let's say that you lot want predicted proportions for some specific combinations of your predictor variables. Specifically, for 500, 600 and 700 for api99, for i and ii for yr_rnd, and for parentrd of 2.v. Yous would suspend the following half dozen observations to your dataset with an n of 4421.
count 4421 fix obs 4427 obs was 4421, now 4427 replace api99 = 500 in 4422 replace api99 = 600 in 4423 supersede api99 = 700 in 4424 replace api99 = 500 in 4425 replace api99 = 600 in 4426 replace api99 = 700 in 4427 replace yr_rnd = one in 4422/4424 replace yr_rnd = two in 4425/4427 supersede parented = ii.5 in 4422/4427 list api99 yr_rnd parented in -6/l, separator(3) +---------------------------+ | api99 yr_rnd parented | |---------------------------| 4422. | 500 No two.five | 4423. | 600 No two.5 | 4424. | 700 No two.5 | |---------------------------| 4425. | 500 Aye 2.5 | 4426. | 600 Yes 2.5 | 4427. | 700 Aye 2.v | +---------------------------+
Rerun your model for the 'real' observations (note the in 1/4421), predict for all observations, and display your results.
glm meals yr_rnd parented api99 in 1/4421, link(logit) family(binomial) robust nolog Generalized linear models No. of obs = 4257 Optimization : ML Remainder df = 4253 Scale parameter = 1 Deviance = 395.8141242 (one/df) Deviance = .093067 Pearson = 374.7025759 (1/df) Pearson = .0881031 Variance function: V(u) = u*(1-u/1) [Binomial] Link role : grand(u) = ln(u/(1-u)) [Logit] AIC = .7220973 Log pseudolikelihood = -1532.984106 BIC = -35143.61 ------------------------------------------------------------------------------ | Robust meals | Coef. Std. Err. z P>|z| [95% Conf. Interval] -------------+---------------------------------------------------------------- yr_rnd | .0482527 .0321714 one.fifty 0.134 -.0148021 .1113074 parented | -.7662598 .0390715 -19.61 0.000 -.8428386 -.6896811 api99 | -.0073046 .0002156 -33.89 0.000 -.0077271 -.0068821 _cons | 6.75343 .0896767 75.31 0.000 6.577667 6.929193 ------------------------------------------------------------------------------ predict premeals (choice mu causeless; predicted mean meals) (164 missing values generated) list api99 yr_rnd parented premeals in -half dozen/l, separator(3) +--------------------------------------+ | api99 yr_rnd parented premeals | |--------------------------------------| 4422. | 500 No 2.5 .774471 | 4423. | 600 No 2.v .6232278 | 4424. | 700 No ii.5 .4434458 | |--------------------------------------| 4425. | 500 Yes ii.5 .7827873 | 4426. | 600 Yeah 2.5 .6344891 | 4427. | 700 Yes two.5 .4553849 | +--------------------------------------+
Source: https://stats.oarc.ucla.edu/stata/faq/how-does-one-do-regression-when-the-dependent-variable-is-a-proportion/
0 Response to "Family to Use in Glm With Very Bimodal Data"
Postar um comentário